Box Counting Dimension Sierpinski Carpet

In fractal geometry the minkowski bouligand dimension also known as minkowski dimension or box counting dimension is a way of determining the fractal dimension of a set s in a euclidean space r n or more generally in a metric space x d it is named after the german mathematician hermann minkowski and the french mathematician georges bouligand.

Box counting dimension sierpinski carpet.

Fractal dimension of the menger sponge. Sierpiński demonstrated that his carpet is a universal plane curve. 4 2 box counting method draw a lattice of squares of different sizes e. The values of these slopes are 1 8927892607 and 1 2618595071 which are respectively the fractal dimension of the sierpinski carpet and the two dimensional cantor set.

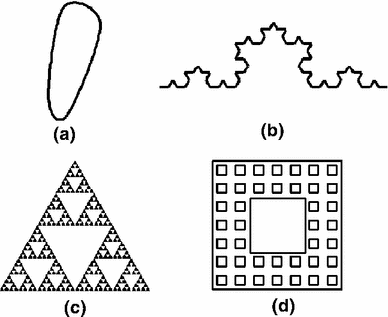
But not all natural fractals are so easy to measure. We learned in the last section how to compute the dimension of a coastline. 111log8 1 893 383log3 d f. This leads to the definition of the box counting dimension.

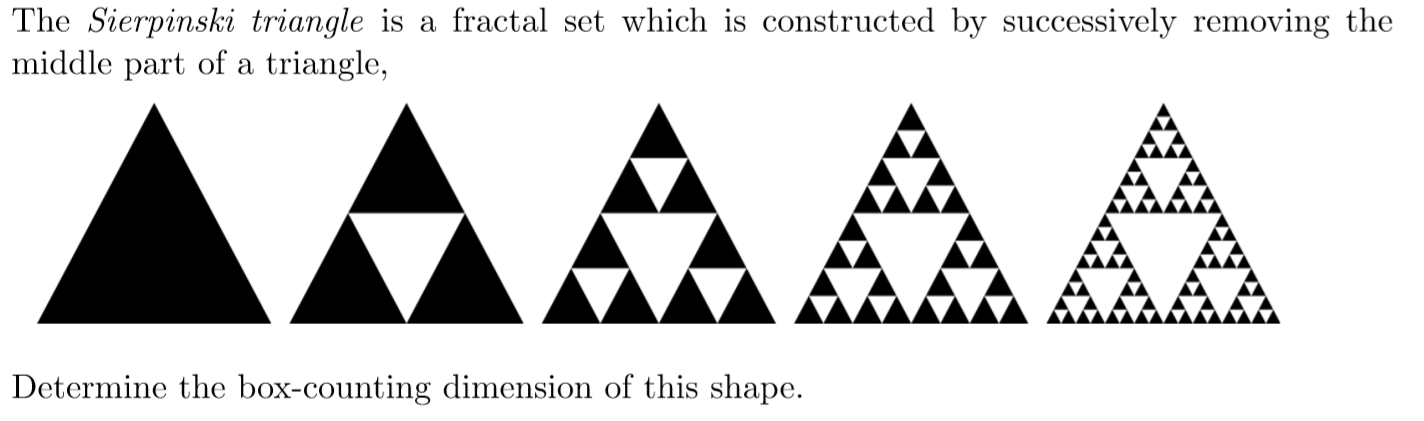
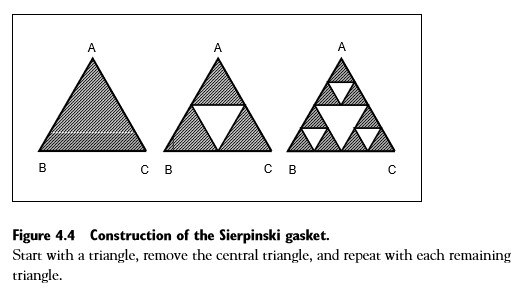
Note that dimension is indeed in between 1 and 2 and it is higher than the value for the koch curve. The gasket is more than 1 dimensional but less than 2 dimensional. It is relatively easy to determine the fractal dimension of geometric fractals such as the sierpinski triangle. The hausdorff dimension of the carpet is log 8 log 3 1 8928.

This makes sense because the sierpinski triangle does a better job filling up a 2 dimensional plane. Box counting analysis results of multifractal objects. The sierpinski carpet is a compact subset of the plane with lebesgue covering dimension 1 and every subset of the plane with these properties is homeomorphic to some subset of the sierpiński carpet. Fractal dimension box counting method.

To calculate this dimension for a fractal. A for the bifractal structure two regions were identified. Next we ll apply this same idea to some fractals that reside in the space between 2 and 3 dimensions.